Answer:
20
Explanation:
Use the distance formula to determine the distance between the two points.
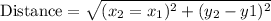
Substitute the actual values of the points into the distance formula.
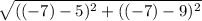
Simplify.
⇒ Subtract 5 from 7.
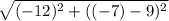
⇒ Raise -12 to the power of 2.
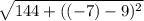
⇒ Subtract 9 from -7.
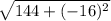
⇒ Raise -16 to the power of 2.
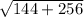
⇒ Add 144 and 256.
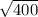
⇒ Rewrite 400 as 20².
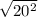
⇒ Pull terms out from under the radical, assuming positive real numbers.
20