Question

Cafeteria A has 7 packs of granola bars and 12 loose granola bars. Cafeteria B has 3 packs of granola bars and 84 loose granola bars. If the cafeterias have

the same number of granola bars, how many are in each package?

Answer 1

Each package has 18 granola bars.

Explanation:

This problem can be solved through a system of linear equations.

1. Form the equations.

Let "x" be the total number of granola bars that each pack of granola has. Let "y" be the total amount of granola bars that each cafeteria has.

For cafeteria A:
`7x+12=y`

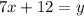
For cafeteria B:
`3x+84=y`

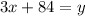
2. Equal the equations.

Since both equations are solved for y, we may take the argument at the left of the equal sign from both equations and equal them.

`7x+12=3x+84`.

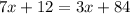3. Solve for x.

`7x+12=3x+84`

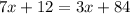
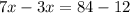`7x-3x=84-12` --> Substract 3x and 12 from both sides.

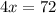`4x=72` --> Simplify by solving the substraction.

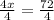`(4x)/(4) =(72)/(4)`--> Divide both sides by 4.

`x= 18`

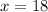
4. Substitute the vallue of x by x on any of the equations.

`y=7(18)+12\\ \\y=138.`

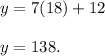
5. Interpret the results.

If a system of linear equations was created, where 2 equations that gave the number of granola bars that each cafeteria has, then the x value obtained when the system was solved, indicates the amount of granola bars that each cafeteria has in each package. Each package has 18 granola bars.