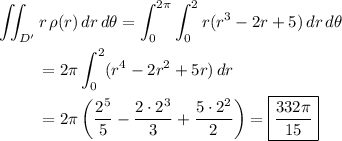Integrate the density over the disk
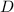 given by
given by
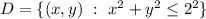
or more conveniently, in polar coordinates by
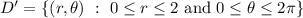
Since the density depends on the distance from the origin, we have
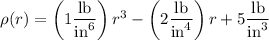
(Note the units in each coefficient ensure that
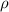 is measured in lb/in³.)
is measured in lb/in³.)
Then the mass (in lb) of the puck is