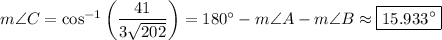Let
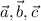 be vectors that point to
be vectors that point to
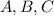 , respectively.
, respectively.
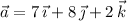
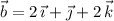
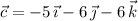
Then consider the directed line segments
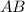 ,
,
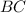 , and
, and
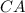 , to which we'll assign the vectors
, to which we'll assign the vectors
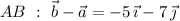
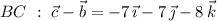
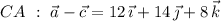
whose lengths are
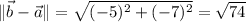
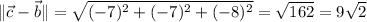
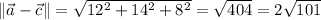
The angle at vertex
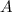 is made by the directed segments
is made by the directed segments
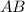 and
and
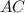 , corresponding to
, corresponding to
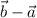 and
and
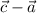 . Use the dot product identity to find the measure of
. Use the dot product identity to find the measure of
 .
.
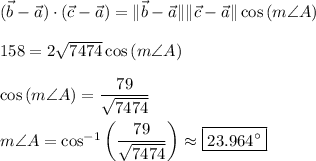
Similarly, the angle at
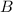 is made by
is made by
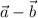 and
and
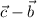 [/tex]. Then
[/tex]. Then
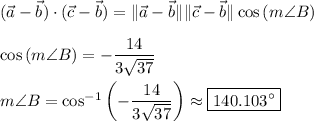
Do the same for
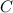 , or simply use the fact that the interior angles in any triangle sum to 180°. You should find
, or simply use the fact that the interior angles in any triangle sum to 180°. You should find