Question

A jazz concert brought in $134,000 on the sale of 8,500 tickets. If the tickets sold for $10 and $20 each, how many of each type of ticket were sold? The number of $10 tickets is?​

Answer 1

3600 $10 tickets

4900 $20 tickets

Explanation:

We can use variables to represent the different types of tickets. Let "x" represent the amount of $10 tickets and "y" represent the amount of $20 tickets. Now we can set up a system of equations.

Setting up a System of Equations

We know that in total, 8500 tickets were sold. Therefore...

`x+y=8500`

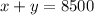
Or in other words, "the amount of $10 tickets plus the amount of $20 tickets is equivalent to 8500 tickets in total".

We also know that $134,000 was made. Therefore...

`10x+20y=134000`

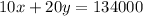
Or in other words, "10 times the amount of $10 tickets plus the 20 times the amount of $20 tickets is equivalent to 134000". Notice that since each ticket costs $10/$20, we have to multiply each variable by that value. We can now solve this system of equations.

Solving the System of Equations

`x+y=8500\\10x+20x=134000`

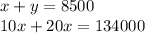
We can solve this system of equations using the elimination method. First, make either the x or y value equivalent in both equations. To do this, we can multiply a whole equation by a certain value.

Multiply the first equation by 10:

`10x+10y=85000\\10x+20y=134000`

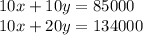
Now, subtract the first equation from the second equation.

`10y=49000`

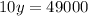
Divide both sides of the equation by 10

`y=4900`

Now, subtract this number from 8500 to find the amount of $10 tickets.

`8500-4900=3600`

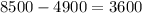
The jazz concert sold 3600 $10 tickets and 4900 $20 tickets.