Question

Rational and Irrational Sums

Rational
Irrational
-4 +23
2/3 + 1/2
-1/4 + 12
2/5 + 15
-3/5 + 6/7
TL + 4
-V3+ 5/8
3.25 +4.17

Answer 1

Rational

Rational

Rational

Rational

Rational

Irrational

Irrational

Rational

Explanation:

First we need to establish what a rational, and a irrational numbers are. A rational number are basically integers that can be written as fractions which means any of the options that are integers or fractions are in fact rational numbers. A irrational number are basically numbers that cannot be written as a fraction which means things like repeating decimals or just numbers that cannot be expressed as a fraction of two other whole numbers.

First option:

`-4+23`

`-4 + 23=19`

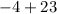
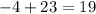
19 is a rational number because it can be expressed as two integers which are 1 and 19

Second option:

`(2)/(3) +(1)/(2)`

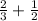
Both are fractions which means the sum will be a fraction which also means it is a rational number since we previously established that every fraction is a rational number.

Third option:

`-(1)/(2) + 12`

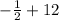
You can write 12 as a fraction which is 12/1 and then solve which the sum will also be a fraction which means it will also be a rational number.

Fourth Option:

`(2)/(5) +15`

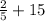
15 can be written as 15/1 which means it is a rational number which also means the sum of the two fractions will also be a rational number.

Fifth option:

Adding fractions, fractions are rational numbers which means the sum will also be a rational number

Sixth option:

Pie is a infinite decimal number which means it is irrational because it cannot be written as a fraction.

Seventh option:

`\sqrt[]{3} +(5)/(8)`

/3 cannot be written as a fraction which means the entire equation is irrational because a rational plus a irrational number will always equal a irrational number.

Eighth option:

`3.25+4.17`

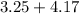
Since how these decimals are not repeating they are both rational numbers.

Hope this helps.