Answer:
Rational
Rational
Rational
Rational
Rational
Irrational
Irrational
Rational
Explanation:
First we need to establish what a rational, and a irrational numbers are. A rational number are basically integers that can be written as fractions which means any of the options that are integers or fractions are in fact rational numbers. A irrational number are basically numbers that cannot be written as a fraction which means things like repeating decimals or just numbers that cannot be expressed as a fraction of two other whole numbers.
First option:
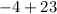

19 is a rational number because it can be expressed as two integers which are 1 and 19
Second option:
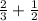
Both are fractions which means the sum will be a fraction which also means it is a rational number since we previously established that every fraction is a rational number.
Third option:

You can write 12 as a fraction which is 12/1 and then solve which the sum will also be a fraction which means it will also be a rational number.
Fourth Option:

15 can be written as 15/1 which means it is a rational number which also means the sum of the two fractions will also be a rational number.
Fifth option:
Adding fractions, fractions are rational numbers which means the sum will also be a rational number
Sixth option:
Pie is a infinite decimal number which means it is irrational because it cannot be written as a fraction.
Seventh option:
![\sqrt[]{3} +(5)/(8)](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/4zpbbfpi4jy9an1fvcea3s.png)
/3 cannot be written as a fraction which means the entire equation is irrational because a rational plus a irrational number will always equal a irrational number.
Eighth option:
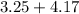
Since how these decimals are not repeating they are both rational numbers.
Hope this helps.