Problem:
A rectangular field is 75 yards wide and 105 yards long. Give the length and width of another rectangular field that has the same perimeter but smaller area.
Answer:
Width: 70 yards.
Length: 110 yards.
Explanation:
1. Extract the value from the original field.
Perimeter:
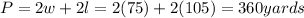 .
.
Area:
 .
.
2. Create a system of equations.
The perimeter must equal 360, hence:
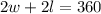 .
.
The area must be below 7875, hence:
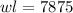
We equal wl to 7875 to find out what values of w or l that can be used to obtain an area lesser than 7875.
3. Isolate variables.
We isolate l on both equations:
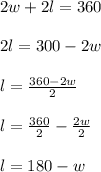
-------------------------------------------------------------------------------------------------------
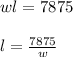
4. Equal the expessions and solve for w.

Use the formula for solving quadratic equations here (check attched image).
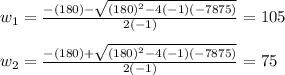
Now, with these values we know that using a width of 75 between 105 and 105 for the field will either maintain the same perimeter and increase the area or maintain perimeter and decrease area. Let's find out which one it is.
4. Finding the relation.
Let's take, for example, the width value of 100. With 100 width, and looking for a perimeter of 360, the length is:
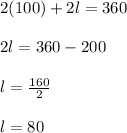
Area is:
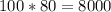
This means that any value of width between 75 and 105 maintains the same perimeter, but increases the area. Therefore, we must choose a value of width that is either lesser than 75 or greater than 105.
5. Establishing the new values.
Using the logic from the last subtitle, let's choose a width of 70, since it's a value out of the interval of 75 and 105, and calculate the length.
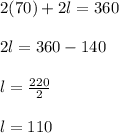
Perimeter stays the same, it's 360 yards,
New area:
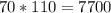
6. Express your results.
The dimensions of a new field that has the same perimeter and smaller area when comparing to the original field are the following:
Width: 70 yards.
Length: 110 yards.
Any value of width below 75 and greater than 105, when it's correct length is found in a way that the perimeter equals 360 yards, should also give an area lesser than the area of the original field.
-------------------------------------------------------------------------------------------------------
Graphical analysis.
(Check the attched images below).
Comments. Check image 3, when we look at this graph, the red area (when x is between 75 and 105) makes the area of the field be above 7875, which is not what we are trying to achieve in this problem. Now, taking values of x that are outside this interval of 75 and 105, the value of the perimeter will stay the same, and the area will decrease.