Question

I run a book club with n people, not including myself. Every day, for 365 days, I invite three members in the club to review a book. What is the smallest positive integer n so that I can avoid ever having the exact same group of three members over all 365 days?

Answer 1

Answer: 15

========================================================

Step-by-step explanation:

The order doesn't matter. A group like {A,B,C} is the same as {B,A,C}.

All that matters is the overall group rather than the positioning of the members.

We'll use the nCr combination formula since order doesn't matter.

The value of n is unknown, but we know that r = 3 members are to be selected.

Let's pick a value for n at random. Let's say n = 10.

Plug n = 10 and r = 3 into the nCr formula below.

`n C r = (n!)/(r!(n-r)!)\\\\10 C 3 = (10!)/(3!*(10-3)!)\\\\10 C 3 = (10!)/(3!*7!)\\\\10 C 3 = (10*9*8*7!)/(3!*7!)\\\\ 10 C 3 = (10*9*8)/(3!)\\\\ 10 C 3 = (10*9*8)/(3*2*1)\\\\ 10 C 3 = (720)/(6)\\\\ 10 C 3 = 120\\\\`

Unfortunately we don't reach 365 or larger.

Let's try n = 11

`n C r = (n!)/(r!(n-r)!)\\\\11 C 3 = (11!)/(3!*(11-3)!)\\\\11 C 3 = (11!)/(3!*8!)\\\\11 C 3 = (11*10*9*8!)/(3!*8!)\\\\ 11 C 3 = (11*10*9)/(3!)\\\\ 11 C 3 = (11*10*9)/(3*2*1)\\\\ 11 C 3 = (990)/(6)\\\\ 11 C 3 = 165\\\\`

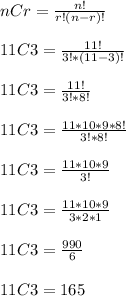
We're still under our target. The good news is that the nCr value is increasing.

So the idea is to do trial and error with various values of n. Keep incrementing n until nCr = nC3 is equal to 365 or larger.

Here's a table of values where r = 3 the entire time

`\begin{array}c \cline{1-2}\text{n} & \text{nCr}\\\cline{1-2}10 & 120\\\cline{1-2}11 & 165\\\cline{1-2}12 & 220\\\cline{1-2}13 & 286\\\cline{1-2}14 & 364\\\cline{1-2}15 & 455\\\cline{1-2}\end{array}`

The nCr values are also found in Pascal's Triangle. Each of those values are the fourth entry of each row.

When n = 14, we have nCr = 364 which is very close. We're one short unfortunately.

So we have to go for n = 15 instead. This makes the nCr value well over 365 of course, but it guarantees that you'll have plenty of trios to choose from such that no group of three is repeated. Unfortunately some trios will be left out.