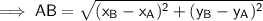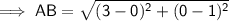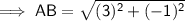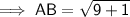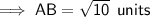Answer:
a) OA = 1 unit
b) OB = 3 units
c) AB = √10 units
Explanation:
Given function:
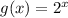
Part (a)
Point A is the y-intercept of the exponential curve (so when x = 0).
To find the y-value of Point A, substitute x = 0 into the function:
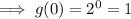
Therefore, A (0, 1) so OA = 1 unit.
Part (b)
If BC = 8 units then the y-value of Point C is 8.
The find the x-value of Point C, set the function to 8 and solve for x:
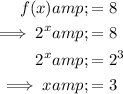
Therefore, C (3, 8) so Point B is (3, 0). Therefore, OB = 3 units.
Part (c)
From parts (a) and (b):
To find the length of AB, use the distance between two points formula:
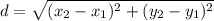
Therefore: