Answer:

Explanation:
Evaluate the difference quotient in the usual way: put the function arguments where the variables are and simplify.
Difference quotient
The formula for the difference quotient is ...
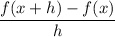
Application
For f(x) = x^3 +2x^2 -5, the difference quotient is ...

__
Additional comment
We have shown h-terms with increasing powers to the right. That is because we're usually concerned with small values of h, so higher-degree terms become insignificant and can be neglected. If the expression were written in "standard form", it might be ...
h^2 +3hx +3x^2 +2h +4x . . . . . lexicographical order of decreasing degree