Question

I need the answer and I need someone to tell me what the dot is by the 3 on the top?

Answer 1

Answer:3

Explanation:

took gtest

Answer 2

6

Explanation:

I'm assuming it's asking what you need to put in the "dot", or in other words what exponent does it have to be, so the two expressions are equal.

Anyways, there's an exponent identity, which essentially states:
`(x^a)/(x^b)=x^(a-b)`

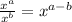
So in this case, let's just say that "dot" is x, to make it a bit easier to express

You have the following equation:
`(3^x)/(3^2)=3^4`

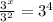
But remember the identity? So it follows that:
`(3^x)/(3^2)=3^(x-2)`

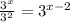
So if we substitute this in, as the fraction we get the equation:
`3^(x-2)=3^4`

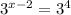
Since the two bases are the same, the exponents have to be the same, so we can write the equation as:
`x-2=4`

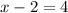
And this is a simple algebraic equation, which you just add 2 to both sides to get:
`x=6`

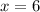
Now, that's not to difficult, but I want to go a bit more in depth as to why the identity:
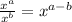`(x^a)/(x^b)=x^(a-b)` intuitively makes sense if you think about it for a bit.

So I can use an abstract example, but I'll use this specific example:
`(3^6)/(3^2)=3^4`

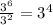
The reason for this, is because if you write out the exponent in multiplication form you get:
`(3*3*3*3*3*3)/(3*3)=3*3*3*3`

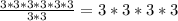
So what we're really doing here, is cancelling out two of the threes. The reason for this is because we have two threes in the numerator, and two in the denominator. So we can just cancel out two of them from the numerator, and this gives us the expression:
`3*3*3*3`

This is just 4 threes being multiplied by each other, which can also be expressed as:
`3^4`

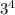
So when you're writing:
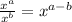`(x^a)/(x^b)=x^(a-b)`, you're just cancelling out x's from the numerator and denominator.