Answer:
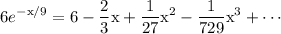
This is the expanded form of
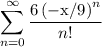
=========================================================
Step-by-step explanation:
f(x) = 6e^(-x/9) is the given function
T(x) = Taylor polynomial function
The goal is to see if we can try to model f(x) in terms of a polynomial T(x).
This means T(x) won't involve the exponential base "e", and it won't have fractional exponents either.
In your notes you should have the following about the Taylor polynomial:
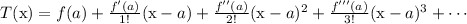
So we'll need to compute the derivatives. Here's the 1st derivative
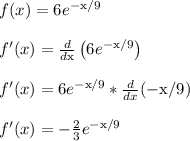
Don't forget about the chain rule.
The second derivative is

I'll skip steps for the third derivative, but you should get

This process is repeated infinitely out; of course realistically we should only do a few derivatives or we'll be here forever.
Here's the summary derivatives we found so far
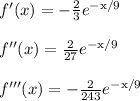
Plug in x = 0 since the Taylor polynomial is centered around here.
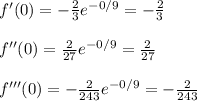
Then we can say:
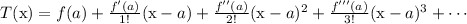
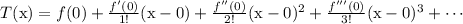
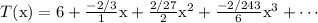

When centered around x = 0, T(x) is a pretty good replacement for f(x). Of course the further you move away from x = 0, is when the error will get worse. I recommend plotting the first few terms of T(x) and f(x) on the same xy grid. You should see the two graphs somewhat merge, or overlap, together around x = 0. The more terms you add onto T(x), the better the approximation will get.
-----------------------------------------
Another approach:
Recall that
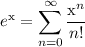
This is a compact way of saying
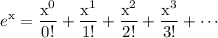
Replace every copy of x with -x/9

Then multiply both sides by 6

If you wanted, you could expand things out a bit
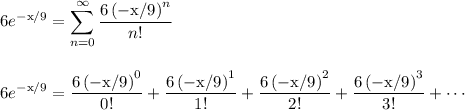
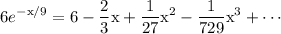
This matches what we found in the previous section.