Question

I’m not sure how to do these two problem if anyone could help on even just one of them I’d appreciate it so much!

Answer 1

• x=2/3, -1/2 ±i√3/2
• x = -1, 0, 1

Explanation:

When in doubt about how to solve a problem, it often works well to follow the instructions.

Solutions to 3x³ +x² = 2 -x

The first attachment shows a graph of the two sides of the equation. The point of intersection is the only real solution: x = 2/3.

The equation is 3rd-degree, so we know it has three solutions. When the equation is written in standard form, it is ...

3x³ +x² +x -2 = 0

The given real solution corresponds to a factor of ...

x -2/3

Multiplying by 3, this factor becomes (3x -2). When that is factored out of the standard form equation, the result is a quadratic factor with complex solutions. (See the second attachment for the division process.)

3x³ +x² +x -2 = (3x -2)(x² +x +1) = 0

The solutions to x² +x +1 = 0 can be found using the quadratic formula:

`x=(-b\pm√(b^2-4ac))/(2a)=(-1\pm√(1^2-4(1)(1)))/(2(1))=(-1\pm i√(3))/(2)`

All of the solutions to 3x³ +x² = 2 -x are ...

`\boxed{x\in\left\{(2)/(3),\ (-1\pm i√(3))/(2)\right\}}`

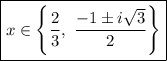
X-intercepts of g(x)

The x-intercepts are where g(x) = 0. The graph in the third attachment shows these handily.

You can also find the x-intercepts by factoring.

g(x) = x³ -x = x(x² -1)

g(x) = x(x -1)(x +1)

Values of x that make these factors zero are x=-1, x=0, x=1.

__

Additional comments

The coefficients of a quadratic in standard form are used in the quadratic formula. That standard form is ax²+bx+c = 0. Comparing this to the given equation, you see that a=1, b=1, c=1.

A product is zero when one or more of its factors is zero. This is the "zero product rule" and is used to find the x-intercepts (zeros, solutions) of a quadratic. The solutions will make one or more of the factors be zero. Of course, the factor (x-a) is zero when x=a.

The factoring of the difference of squares is ...

a² -b² = (a -b)(a +b)