Answer:
4 and 5
Explanation:
For answering questions like this, it can be useful to remember a few of the powers of small integers:
2^4 = 16
2^5 = 32
Exponents and logarithms
A logarithm can be considered to be an exponent of the base.
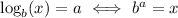
The ordering of powers of 2 relative to the number of interest (17) is ...
16 < 17 < 32
2⁴ < 17 < 2⁵ . . . . . . . . . . . . . . . . . . . expressed as powers of 2
log₂(2⁴) < log₂(17) < log₂(2⁵) . . . . . log₂ of the above inequality
4 < log₂(17) < 5 . . . . . . . . . . . . . . . . showing the values of the logs
Log₂(17) lies between 4 and 5.
__
Additional comment
Using the "change of base" formula, you can use a calculator to find the value of log₂(17). It shows you the value is between 4 and 5.
log₂(17) = log(17)/log(2) . . . . . . using logs to the same base