Question

Solve the system below using elimination
{5x+9y= -10}
{7x+10y= -1}

Answer 1

∑Hey , jillianwagler ⊃

Answer:

x = 7, y = -5

Explanation:

Given~:

Solve the system below using elimination

{5x+9y= -10}

{7x+10y= -1}

Solve:

`\begin{bmatrix}5x+9y=-10\\ 7x+10y=-1\end{bmatrix}`

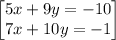
Isolate x ( 5x + 9y = -10 ) :
`\mathrm{x=(-10-9y)/(5)}`

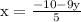
Substitute:
`\mathrm{x=(-10-9y)/(5)}`

`\begin{bmatrix}7\cdot (-10-9y)/(5)+10y=-1\end{bmatrix}`

`\begin{bmatrix}(-70-13y)/(5)=-1\end{bmatrix}`

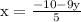
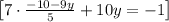
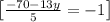
Isolate y :
`(-70-13y)/(5)=1:y=-5`

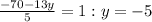
Substitute:
`y=-5`

`x=(-10-9\left(-5\right))/(5)=7`

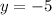
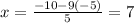
Hence,
`x=7`

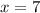
Therefore, the solution for
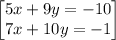`\begin{bmatrix}5x+9y=-10\\ 7x+10y=-1\end{bmatrix}` are:

`x=7,\:y=-5`

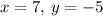
xcookiex12

8/19/2022