Notice that if both
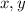 are positive, then
are positive, then
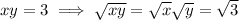
We also have the binomial expansion
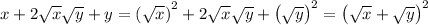
Then
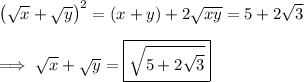
Let's see if we can denest the radical. Suppose we could write
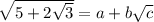
for some non-zero integer constants
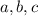 (and
(and
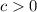 ). Squaring both sides gives
). Squaring both sides gives
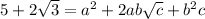
Let
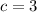 and
and
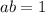 . Then
. Then
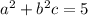 , which gives
, which gives
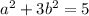
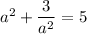
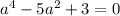
We can solve this with the quadratic formula. However, it'll lead to non-integer solutions for
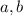 , so we cannot denest after all.
, so we cannot denest after all.