Answer:
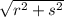
=====================================================
Reason:
Plot the points (0,0) and (r,s). You can place (r,s) anywhere you want.
Connect the two points mentioned and form a right triangle such that the segment from (0,0) to (r,s) is the hypotenuse of said right triangle.
The horizontal leg has a length of r-0 = r units, while the vertical leg will be 's' units.
Check out the diagram below.
We then apply the pythagorean theorem to say
 where h is the hypotenuse. Solving for h gets us
where h is the hypotenuse. Solving for h gets us
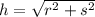 . We only focus on the positive square root since a negative hypotenuse makes no sense.
. We only focus on the positive square root since a negative hypotenuse makes no sense.
Since we made the hypotenuse the segment with endpoints (r,s) and (0,0), this means the hypotenuse length and the distance are the same thing.
Therefore, the distance from (r,s) to (0,0) is
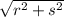
As an alternative, you can use the distance formula to get the same answer. The distance formula is effectively the pythagorean theorem phrased a different way.