Answer:
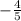 .
.
Explanation:
1. Find the slope of the given equation.
To find this value, we need to solve the equation for y.
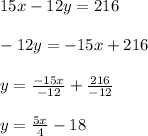
The slope of a linear equation is always the number by which the x in being multiplied when the equation is solved for y. Hence, the value of the slope is
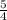 .
.
2. Find slope of the original line.
The problem gives us information to find the slope of the line perpendicular to
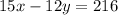 . Since the slope of the given equation is
. Since the slope of the given equation is
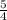 , the slope of a perpendicular line is the multiplicative reciprocal with the opposite sign. This is inverting the fraction, and adding the opposite symbol of what the original fraction had, like this:
, the slope of a perpendicular line is the multiplicative reciprocal with the opposite sign. This is inverting the fraction, and adding the opposite symbol of what the original fraction had, like this:
a. We invert the fraction.
We previously had
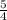 , now we'll have
, now we'll have
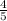
b. Add the opposite sign before the fraction.
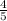 doesn't have a sign before it, that means that it is positive. Converting it to negative we have
doesn't have a sign before it, that means that it is positive. Converting it to negative we have
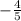 .
.
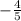 is our final answer.
is our final answer.