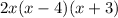Question

100 POINTS

Factor Completely:

The second equation

Answer 1

`2x(x-4)(x+3)`.

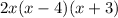Explanation:

1. Write the expression.

`2x^(3) -2x^(2) -24x`

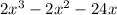
2. Divide all terms by a common term.

A common term is a term that can divide all the terms without leaving a denominator or a residue.

`(2x^(3))/(2x) -(2x^(2) )/(2x) -(24x)/(2x)`

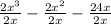
3. Rewrite.

`2x(x^(2) -x-12)`

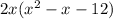
4. Find 2 values that summed up equal -1 and multiplied equal -12.

This is because the coefficient of x is -1 and the coefficient of -12 is itself, -12.

-4 and 3 are two values that meet these requirements.

Note. This method doesn't always work for factorizing an expression, you may need to refer to other methods to solve these problems. A different method would be finding a solution for the quadratic formula throgh the quadratic formula. You may research a little more about this topic and how to use the quadratic formula on the internet.

5. Take the value we divided by on step 2 and type the found values in the following fashion.

`2x(x-4)(x+3)`

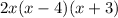
6. Express a result.

`2x(x-4)(x+3)`