Question

An elevator containing five people can stop at any of seven floors. What is the probability that no two people exit at the same floor

Answer 1

Approximately
`0.15` (
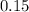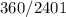`360 / 2401`.) (Assume that the choices of the
`5` passengers are independent. Also assume that the probability that a passenger chooses a particular floor is the same for all
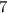`7` floors.)

Explanation:

If there is no requirement that no two passengers exit at the same floor, each of these
`5` passenger could choose from any one of the
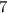`7` floors. There would be a total of
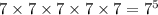`7 * 7 * 7 * 7 * 7 = 7^(5)` unique ways for these
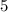`5\!` passengers to exit the elevator.

Assume that no two passengers are allowed to exit at the same floor.

The first passenger could choose from any of the
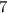`7` floors.

However, the second passenger would not be able to choose the same floor as the first passenger. Thus, the second passenger would have to choose from only
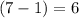`(7 - 1) = 6` floors.

Likewise, the third passenger would have to choose from only
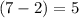`(7 - 2) = 5` floors.

Thus, under the requirement that no two passenger could exit at the same floor, there would be only
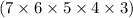`(7 * 6 * 5 * 4 * 3)` unique ways for these two passengers to exit the elevator.

By the assumption that the choices of the passengers are independent and uniform across the
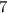`7` floors. Each of these
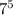`7^(5)` combinations would be equally likely.

Thus, the probability that the chosen combination satisfies the requirements (no two passengers exit at the same floor) would be:

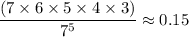`\begin{aligned}((7 * 6 * 5 * 4 * 3))/(7^(5)) \approx 0.15\end{aligned}`.