Answer:
0.85 m/s²
Step-by-step explanation:
Acceleration is change in velocity over change in time. In mathematically, it can be expressed as:
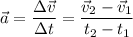
Our final velocity is given to be 17 m/s in 20 seconds. Initial velocity is at starting point which is 0 m/s in 0 second. Therefore:
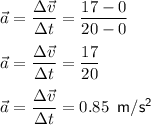
Therefore, the acceleration of a horse from starting point to 17 m/s in 20 seconds is 0.85 m/s²