Answer:

Explanation:
The infinite series sum of a converging geometric series is:
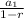
A geometric sequence can generally be defined as:

The series you provided, seems to be oscillating from negative to positive values. What this is telling us, is that the "r" value or what's being multiplied from one term to another, is negative.
We know this because take for example:
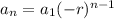
When n=1:

When n=2:

When n=3:
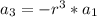
When n=4:
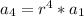
Basically, when the degree is odd the negative sign isn't cancelled out, but when the degree is even, the negative signs can be "paired" in groups of twos in which they cancel out resulting in a positive number. So it will be positive then negative then positive then negative and so on...
So we know that r is negative, but what is the magnitude of r?
Well we can find this by dividing one value by the previous value.

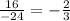
Also we didn't really need to analyze the series to see that "r" was negative, we could've just divided. I just wanted to clarify as to why "r" is negative.
Anyways moving on, as given in the series the first term is 36, so:
 and
and
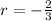
This gives us a sum of:
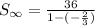
Cancel out the negatives:
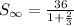
Rewrite the 1 as 3/3:
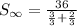
Combine the denominator into one fraction:
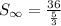
Keep, change, flip:
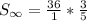
Multiply Values:

This is our answer.