Question

What is the equation of a line that passes through (8,-5) and is parallel to the graphed line?

Answer 1

What is an equation of the line that passes through the point (-5,8) and is parallel to the line x + y = 8?

Equation of a Line:

There are different ways in solving for the equation of a line depending on the given values. The slope-intercept form can be used when the slope and y-intercept are given. Also, the point-slope form can be used when the slope and a point in the line are given.

Answer and Explanation: 1

Given:

a line that passes through the point

(

−

5

,

8

)

where

x

1

=

−

5

and

y

1

=

8

parallel to the line

x

+

y

=

8

Since parallel lines has the same slope, we solve for the slope of the equation

x

+

y

=

8

by transforming it to its slope-intercept form

y

=

m

x

+

b

where

m

is the slope.

x

+

y

=

8

y

=

−

x

+

8

m

=

−

1

Now, we have a slope

(

m

=

−

1

)

and a point in the line

(

x

1

=

−

5

,

y

1

=

8

)

, we can write an equation of the line using the point-slope form

y

−

y

1

=

m

(

x

−

x

1

)

y

−

y

1

=

m

(

x

−

x

1

)

y

−

8

=

−

1

(

x

−

(

−

5

)

)

y

−

8

=

−

1

(

x

+

5

)

y

−

8

=

−

(

x

+

5

)

Therefore, the equation of the line can be written as

y

−

8

=

−

(

x

+

5

)

Answer 2

The equation of the line that passes through the given points and is parallel to the graphed line is
`\[y = (3)/(4)x - 11\]`

How to find the equation ?

In the given line, you have two points: (-4, -6) and (8, 3). You can calculate the slope (m) of the given line using the formula:

`\[m = (y_2 - y_1)/(x_2 - x_1)\]`

Using the points (-4, -6) and (8, 3):

`\[m = (3 - (-6))/(8 - (-4)) = (9)/(12) = (3)/(4)\]`

Now that you have the slope (m = 3/4) of the given line, you can use it to find the equation of the line parallel to it and passing through the point (8, -5). The equation of a line in point-slope form is:

`\[y - y_1 = m(x - x_1)\]`

Using the point (8, -5) and the slope m = 3/4:

`\[y - (-5) = (3)/(4)(x - 8)\]`

`\[y + 5 = (3)/(4)(x - 8)\]`

`\[y + 5 = (3)/(4)x - 6\]`

`\[y = (3)/(4)x - 6 - 5\]`

y = 3 / 4 x - 11

In conclusion, the equation of the line that passes through (8, -5) and is parallel to the given line is
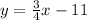`\(y = (3)/(4)x - 11\)`.