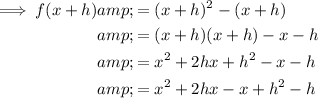Question

Can someone please help I’m not sure how to solve 3 and 4 I’m also not even sure if 1 or 2 is right. Please give an explanation! 50 points

Answer 1

`\textsf{1)} \quad f(2)=2`

`\textsf{2)} \quad 2f(x)=2x^2-2x`

`\textsf{3)} \quad f(2+h)=h^2+3h+2`

`\textsf{4)} \quad f(x+h)=x^2+2hx-x+h^2-h`

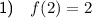
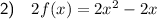
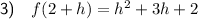
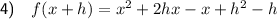
Explanation:

Given function:

`f(x)=x^2-x`

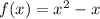
Question 1

To find f(2) substitute x = 2 into the given function:

`\begin{aligned}\implies f(2) & = (2)^2-2\\& = 4-2\\& = 2\end{aligned}`

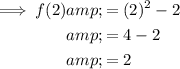
Question 2

To find 2f(x) multiply the given function by 2:

`\begin{aligned}\implies 2f(x) & = 2(x^2-x)\\& = 2x^2-2x\end{aligned}`

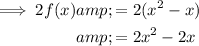
Question 3

To find f(2 + h) substitute x = 2 + h into the given function:

`\begin{aligned}\implies f(2+h) & = (2+h)^2-(2+h)\\& = (2+h)(2+h)-2-h\\& = 4+4h+h^2-2-h\\ & = h^2+4h-h+4-2\\& = h^2+3h+2\end{aligned}`

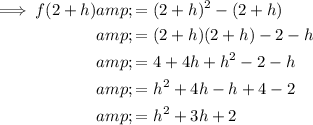
Question 4

To find f(x + h) substitute x = x + h into the given function:

`\begin{aligned}\implies f(x+h) & = (x+h)^2-(x+h)\\& = (x+h)(x+h)-x-h\\& = x^2+2hx+h^2-x-h\\& = x^2+2hx-x+h^2-h\end{aligned}`