1. According to the plot, this happens twice for some
 between 135° and 180°, and for some
between 135° and 180°, and for some
 between 270° and 315°.
between 270° and 315°.
We could try finding them exactly, but we would end up having to solve a 4th degree polynomial equation that doesn't factorize nicely...
2. Rewrite the inequality as
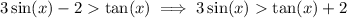
The curve
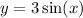 lies above
lies above
 when
when
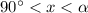 , where
, where
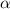 is the first solution mentioned in (1) between 135° and 180°, approximately
is the first solution mentioned in (1) between 135° and 180°, approximately
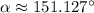 .
.
3. Rewriting
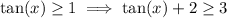
we see from the plot that this is true for
 between 45° and 90°, and again between 225° and 270°.
between 45° and 90°, and again between 225° and 270°.