1. I'm not sure how you're expected to "read off" where they intersect based on an imprecise hand-drawn graph, but we can still find these intersections exactly.
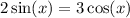
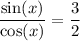
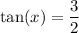
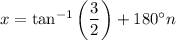
where
 is an integer.
is an integer.
In the interval [0°, 360°], we have solutions at
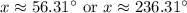
From the sketch of the plot, we do see that the intersections are roughly where we expect them to be. (The first is somewhere between 45° and 90°, while the second is somewhere between 225° and 270°.)
2. According to the plot and the solutions from (1), we have
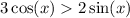
whenever
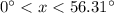 or
or
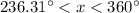 .
.
3. Rewrite the inequality as
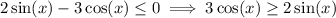
The answer to (1) tells us where the equality
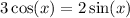 holds.
holds.
The answer to (2) tells us where the strict inequality
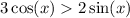 holds.
holds.
Putting these solutions together, we have
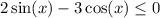 whenever
whenever
 or
or
 .
.