Answer: the cost of each balloon is $1, the cost of each banner is $2.
Explanation:
Let the cost of each balloon is x, and the cost of each banner is y.
Hence,

We multiply equation (1) by -2:
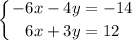
Let's sum up these equations:
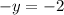
Multiply both sides of the equation by -1:
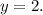
We substitute the value of y into equation (1):
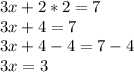
Divide both sides of the equation by 3:
