Answer:
35 and 28.
Explanation:
This problem can be solved using a system of linear equations.
Let one number be x and the other be y.
"The ratio of two numbers is 5 to 4", therefore:
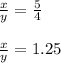
Also, "...the sum of the numbers is 63", therefore:

1. Set up the linear equations system.
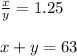
2. Take the value of one of the variables from one of the equations.
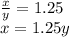
3. Substitute this value into the other equation and solve for y.

4. Now that we have a value for y, take an equation and find the value of x.

Therefore, our 2 numbers are 35 and 28.