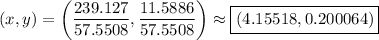The coordinates of the centroid are the average values of the
 - and
- and
 -coordinates of the points
-coordinates of the points
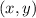 that belong to the region. Let
that belong to the region. Let
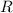 denote the bounded region. These averages are given by the integral expressions
denote the bounded region. These averages are given by the integral expressions
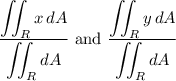
The denominator is just the area of
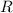 , given by
, given by
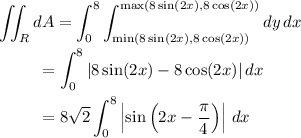
where we rewrite the integrand using the identities

Now, if
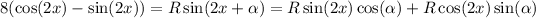
with
 , then
, then
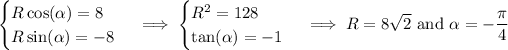
Find where this simpler sine curve crosses the
 -axis.
-axis.
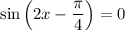

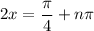
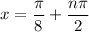
In the interval [0, 8], this happens a total of 5 times at
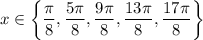
See the attached plots, which demonstrates the area between the two curves is the same as the area between the simpler sine wave and the
 -axis.
-axis.
By symmetry, the areas of the middle four regions (the completely filled "lobes") are the same, so the area integral reduces to
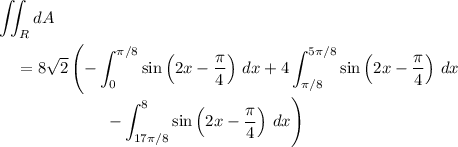
The signs of each integral are decided by whether
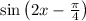 lies above or below axis over each interval. These integrals are totally doable, but rather tedious. You should end up with
lies above or below axis over each interval. These integrals are totally doable, but rather tedious. You should end up with
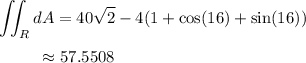
Similarly, we compute the slightly more complicated
 -integral to be
-integral to be
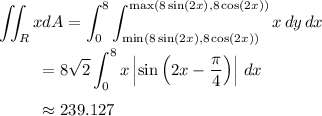
and the even more complicated
 -integral to be
-integral to be
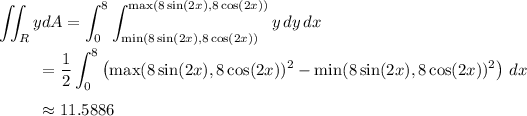
Then the centroid of
 is
is