Let
 be the smallest of the 4 integers, so the others are
be the smallest of the 4 integers, so the others are
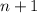 ,
,
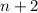 , and
, and
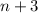 . Their product is
. Their product is
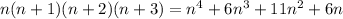
Now consider the statement
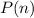 that says
that says
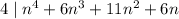
(i.e. 4 divides the quartic)
Check the base case
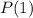 .
.

and 4 | 24 since 24 = 4•6
Now assume
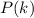 is true. We want to use it to show
is true. We want to use it to show
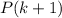 is also true. This requires proving
is also true. This requires proving
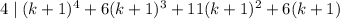
assuming that
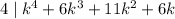
Expand the quartic expression completely.
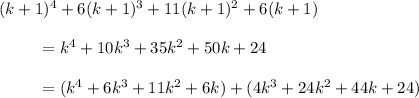
The first group of terms is divisible by 4 thanks to the assumption
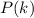 . The second group of terms is clearly divisible by 4, since each coefficient is a multiple of 4. So
. The second group of terms is clearly divisible by 4, since each coefficient is a multiple of 4. So
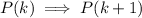 . QED
. QED