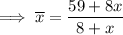Question

Median and the mode.

Medications are essential expenses. DeWitt has
composed a price list of antibiotics available at
ifferent pharmacies in his neighborhood. In
eviewing his list, he can't find the number of
harmacies selling the antibiotics for $8. Examine
me frequency distribution for the prices. Write an
pression for the mean.

Price Frequency
$4.10 3
$4.85 2
$8.00 x
$12.00 1
$12.50 2

Answer 1

`\overline{x}=(59+8x)/(8+x)`

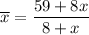
Explanation:

Mean: The sum of all data values divided by the total number of data values.

Create a frequency table with the given information.

Label Price as "x" and Frequency as "f".

Add an "fx" column and enter the values of f multiplied by x.

Add a "Total" row and enter the total frequency and total fx.

`\begin{array}c\cline{1-3}\sf Price & \sf Frequency &\\x & f & fx\\\cline{1-3} 4.10 & 3 & 12.3 \\\cline{1-3} 4.85 & 2 & 9.7 \\\cline{1-3} 8.00 & x & 8x \\\cline{1-3} 12.00 & 1 & 12 \\\cline{1-3} 12.50 & 2 & 25 \\\cline{1-3} \sf Total & 8+x & 59+8x\\\cline{1-3}\end{array}`

The formula for the mean is:

`\boxed{\text{Mean}= \overline{x} = (\displaystyle \sum fx)/(\displaystyle \sum f)}`

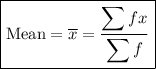
where:

• x = data value
• f = frequency of each x

The Sigma sign means "sum".

Substitute the totals into the formula to create an expression for the mean:

`\implies \overline{x}=(59+8x)/(8+x)`

Answer 2

`\boxed{\bold{\green{(59+8x)/(8+x)}}}`

Answer:

Solution Given:

The expression of the mean =
`\frac{sum \:\:of \:\:price*frequency} {sum\:\: of \:\:frequency}`

=
`(4.10*3+4.85*2+8*x+12*1+12.5*2)/(3+2+x+1+2)`

=
`\boxed{\bold{\green{(59+8x)/(8+x)}}}` is a required expression.