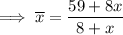Answer:
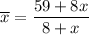
Explanation:
Mean: The sum of all data values divided by the total number of data values.
Create a frequency table with the given information.
Label Price as "x" and Frequency as "f".
Add an "fx" column and enter the values of f multiplied by x.
Add a "Total" row and enter the total frequency and total fx.

The formula for the mean is:
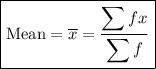
where:
- x = data value
- f = frequency of each x
The Sigma sign means "sum".
Substitute the totals into the formula to create an expression for the mean: