Question

HELP ASAP PLEASE

Given the system of equations:


2x − y = −2


x= 14 + 2y


What is the value of the system determinant?


What is the value of the y−determinant?


What is the value of the x−determinant?


What is the solution to the system of equations?


Show all of your work.

Answer 1

solution: (x, y) = (-6, -10)

(see below for the "work")

Explanation:

You are asked for the solution following the steps of evaluating Cramer's Rule.

System of equations in matrix form

Subtracting 2y from the second equation puts it in standard form, so the system is ...

• 2x -y = -2
• x -2y = 14

Then the matrix equation is ...

`\mathbf{AX}=\mathbf{B}\\\\\left[\begin{array}{cc}2&-1\\1&-2\end{array}\right] \left[\begin{array}{c}x\\y\end{array}\right] =\left[\begin{array}{c}-2\\14\end{array}\right]`

Determinant

The system determinant (Δ) is the determinant of the matrix of the coefficients of the variables.

`\left|\begin{array}{cc}2&-1\\1&-2\end{array}\right|=(2)(-2)-(1)(-1)=-4+1=\boxed{-3}`

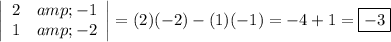
Y-determinant

The y-determinant (Δy) is the determinant of the matrix with the y-coefficients replaced by the constants (B).

`\left|\begin{array}{cc}2&-2\\1&14\end{array}\right|=(2)(14)-(1)(-2)=28+2=\boxed{30}`

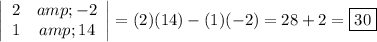
X-determinant

The x-determinant (Δx) is the determinant of the matrix with the x-coefficients replaced by the constants (B).

`\left|\begin{array}{cc}-2&-1\\14&-2\end{array}\right|=(-2)(-2)-(14)(-1)=4+14=\boxed{18}`

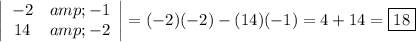
Solution

The solution is the ratio of the appropriate determinants:

x = Δx/Δ = 18/-3 = -6

y = Δy/Δ = 30/-3 = -10

The solution is (x, y) = (-6, -10).

__

The attachment shows a matching graphical solution.