Question

How many 11-digit positive integers can be written using only the digits 1,2, and 3, and have exactly five 1’s and exactly two 2's as digits?

Answer 1

6930

Explanation:

If a 11 digit number contains exactly five 1's and exactly two 2's (and the remaining only 3's),

We can choose the positions of the 1's in
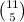`11 \choose 5` ways.

We can select the positions of the two 2's from the 6 remaining positions in
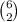`6 \choose 2` ways.

That leaves 11-(5+2) = 4 spots for the remaining numbers which must be all 3's. This can be done in
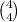`4 \choose 4` ways

So total number of ways this can be done is

`{11 \choose 5} {6 \choose 2}{4 \choose 4}`

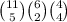
Noting that
`{n \choose k} = (n!)/(k!(n-k)!)`

`{11 \choose 5} = (11!)/(5!(11-5)!) = (11!)/(5!6!) \\{6 \choose 2} = (6!)/(2!(6-2)!) = (6!)/(2!4!) \\{4\choose 4} = (4!)/(4!(4-4)!) = (4!)/(4!0!)`

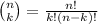
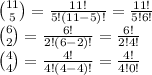
So answer =
`(11!)/(5!6!) (6!)/(2!4!)(4!)/(4!0!)` =
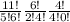`(11!)/(5!2!4!)` since 0! = 1

This evaluates to 6930