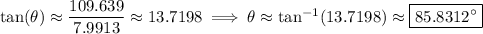Question

A person walks 50 m at 40°, 95 m at 90°, then 35 m at 210°. Calculate the net displacement,

including direction.

Answer 1

Write each displacement vector in component form.

First displacement:

`\vec v_1 = (50\,\mathrm m) (\cos(40^\circ) \,\vec\imath + \sin(40^\circ)\,\vec\jmath) \approx (38.3022\,\vec\imath + 32.1394\,\vec\jmath)\,\mathrm m`

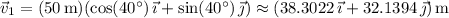
Second displacement:

`\vec v_2 = (95\,\mathrm m) (\cos(90^\circ) \,\vec\imath + \sin(90^\circ)\,\vec\jmath) = (95\,\vec\jmath) \, \mathrm m`

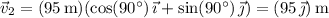
Third displacement:

`\vec v_3 = (35\,\mathrm m) (\cos(210^\circ) \,\vec\imath + \sin(210^\circ) \,\vec\jmath) \approx (-30.3109\,\vec\imath - 17.5\,\vec\jmath) \,\mathrm m`

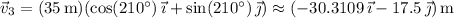
Compute the resultant to get the net displacement vector.

`\vec v_1 + \vec v_2 + \vec v_3 \approx (7.9913\,\vec\imath + 109.639\,\vec\jmath) \, \mathrm m`

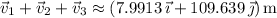
The net displacement is the magnitude of this vector,

`\|\vec v_1 + \vec v_2 + \vec v_3\| = √((7.9913\,\mathrm m)^2 + (109.639\,\mathrm m)^2) \approx \boxed{109.93\,\mathrm m}`

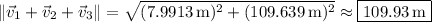
Both components of the vector are positive, so the angle made by the resultant is between 0° and 90°, and

`\tan(\theta) \approx (109.639)/(7.9913) \approx 13.7198 \implies \theta \approx \tan^(-1)(13.7198) \approx \boxed{85.8312^\circ}`