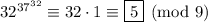Recall Euler's theorem: if
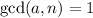 , then
, then
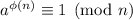
where
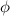 is Euler's totient function.
is Euler's totient function.
We have
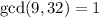 - in fact,
- in fact,
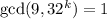 for any
for any
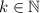 since
since
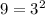 and
and
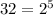 share no common divisors - as well as
share no common divisors - as well as
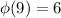 .
.
Now,
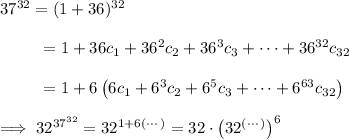
where the
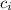 are positive integer coefficients from the binomial expansion. By Euler's theorem,
are positive integer coefficients from the binomial expansion. By Euler's theorem,
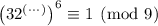
so that