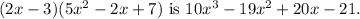Final Answer:
Fiona expanded the product of the binomial
 and the trinomial
and the trinomial
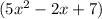 using the FOIL method (First, Outer, Inner, Last). The result of this multiplication is the polynomial
using the FOIL method (First, Outer, Inner, Last). The result of this multiplication is the polynomial

Step-by-step explanation:
Fiona followed the FOIL method to multiply each term of the binomial
 by each term of the trinomial
by each term of the trinomial
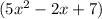 . Here's the step-by-step calculation:
. Here's the step-by-step calculation:
1. First: Multiply the first terms of each binomial:
![\[ (2x) \cdot (5x^2) = 10x^3 \]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/middle-school/acq2dzeawyrx0ms3pc14t9.png)
2. Outer: Multiply the outer terms:
![\[ (2x) \cdot (-2x) = -4x^2 \]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/middle-school/xyedhoxw58hlzyw56iysk4.png)
3. Inner: Multiply the inner terms:
![\[ (-3) \cdot (5x^2) = -15x^2 \]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/middle-school/4iagphnrfimdb0qhzq6agr.png)
4. Last: Multiply the last terms of each binomial:
![\[ (-3) \cdot (-2x) = 6x \]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/middle-school/o5sa2dvqejku5q1newfi3b.png)
Now, combine all the terms:
![\[ 10x^3 - 4x^2 - 15x^2 + 6x - 21 \]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/middle-school/1bjy3h30h6pvanannfp8gr.png)
Combine like terms:
![\[ 10x^3 - 19x^2 + 20x - 21 \]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/middle-school/cb552c8q60gxw6ugj5sj9x.png)
So, the expanded form of