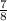Question

in a geometric progression, the sum to infinity is equal to 8 times the first term. Find the common ration.​

Answer 1

r =
`(7)/(8)`

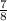
Explanation:

the sum to infinity of a geometric progression is

S∞ =
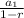`(a_(1) )/(1-r)` : | r | < 1

where a₁ is the first term and r the common ratio

given S∞ = 8a₁ , then

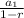`(a_(1) )/(1-r)` = 8a₁ ( multiply both sides by 1 - r )

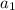`a_(1)` = 8a₁(1 - r) ( divide both sides by 8a₁ )

`(a_(1) )/(8a_(1) )` = 1 - r

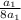`(1)/(8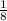)` = 1 - r ( subtract 1 from both sides )

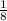`(1)/(8)` - 1 = - r

`(1)/(8)` -
`(8)/(8)` = - r

-
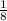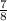`(7)/(8)` = - r ( multiply both sides by - 1 ) , then

r =
`(7)/(8)`