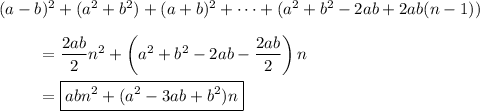Question

1. Find the sum of the following AP (i) 2, 4, 6, ... to n terms (ii) 7, 71, 72, 73, ... to 50 terms (iii) a, (a + b), (a + 2b), ... to n terms (iv) x + y, x-y, x-3y,... to 20 terms (v) (a - b)², (a² + b2), (a + b)², ... to n terms.​

Answer 1

Let
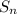`S_n` be the sum of the first
`n` natural numbers.

`S_n = 1 + 2 + 3 + \cdots + n`

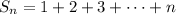
We can reverse the order of terms to write

`S_n = n + (n-1) + (n-2) + \cdots + 1`

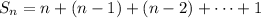
so that doubling up, we get

`2S_n = (1 + n) + (2 + (n-1)) + (3 + (n-2)) + \cdots + (n + 1)`

`2S_n = (n + 1) + (n + 1) + (n + 1) + \cdots + (n + 1)`

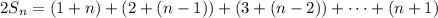
and since there are
`n` terms in
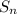`S_n`, it follows that

`2S_n = n(n+1) \implies S_n = \frac{n(n+1)}2`

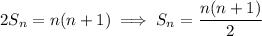
Now, for an arithmetic sequence starting with
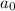`a_0` and having common difference
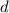`d` between consecutive terms, the sum of the first
`n` terms of this sequence is

`a_0 + (a_0 + d) + (a_0 + 2d) + \cdots + (a_0 + (n-1)d) \\\\ ~~~~~~~~ = (a_0 - d + d) + (a_0 - d + 2d) + (a_0 - d + 3d) + \cdots + (a_0 - d + nd) \\\\ ~~~~~~~~ = (a_0 - d) n + d S_n \\\\ ~~~~~~~~ = \frac d2 n^2 + \left(a_0 - \frac d2\right) n`

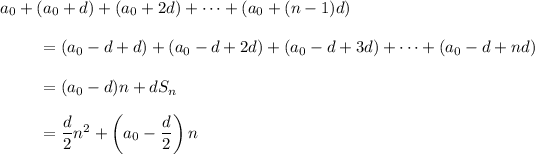
(i) This sum is simply

`2 + 4 + 6 + \cdots + 2n \\\\ ~~~~~~~~ = 2 (1 + 2 + 3 + \cdots + n) \\\\ ~~~~~~~~ = 2 S_n \\\\ ~~~~~~~~ = \boxed{n(n+1)}`

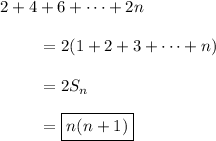
(ii) The first term in this sequence should be 70 if it's arithmetic. The common difference is then 1, the 50th term is 70 + (50 - 1)•1 = 119, so

`70 + 71 + 72 + \cdots + 119 \\\\ ~~~~~~~~ = \frac12\cdot50^2 + \left(70 - \frac12\right)\cdot50 \\\\ ~~~~~~~~ = \boxed{4725}`

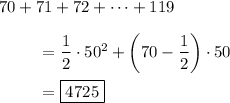
(iii) The first term is
`a` and the common difference is
`b`, so

`a + (a + b) + (a + 2b) + \cdots + (a + b(n-1)) \\\\ ~~~~~~~~ = \boxed{\frac b2 n^2 + \left(a - \frac b2\right)n}`

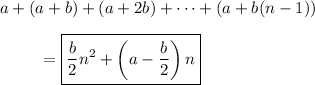
(iv) The first term is
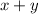`x+y` and the common difference is
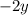`-2y`. Then the 20th term in the sequence is
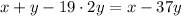`x+y - 19\cdot2y= x-37y`, so

`(x + y) + (x - y) + (x - 3y) + \cdots + (x - 37y) \\\\ ~~~~~~~~ = -\frac{2y}2\cdot20^2 + \left(x + y + \frac{2y}2\right)\cdot20 \\\\ ~~~~~~~~ = \boxed{20x - 360y}`

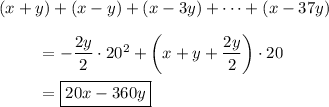
(v) Note that the first term is

`(a - b)^2 = a^2 + b^2 - 2ab`

so that the common difference is
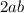`2ab`. Then

`(a - b)^2 + (a^2 + b^2) + (a + b)^2 + \cdots + (a^2 + b^2 - 2ab + 2ab(n-1)) \\\\ ~~~~~~~~ = \frac{2ab}2 n^2 + \left(a^2 + b^2 - 2ab - \frac{2ab}2\right) n \\\\ ~~~~~~~~ = \boxed{abn^2 + (a^2 - 3ab + b^2)n}`