Question

How do you find the end behavior of a rational equation?
Algebra 2

Answer 1

Step 1:

Check the numerator and denominator's degrees. The behavior of the function ends at a horizontal asymptote of
`y=0` if the degree of the denominator is greater than the degree of the numerator.

Step 2:

There is a horizontal asymptote of
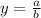`y = (a)/(b)`, where an is the leading coefficient of the numerator and b is the leading coefficient of the denominator, if the degrees of the numerator and denominator are equal. The final behavior is this.

Step 3:

If the degree of the numerator exceeds the degree of the denominator, either the function asymptotes to a polynomial or there is a slant/oblique asymptote (if the degree of the numerator is precisely one bigger than the degree of the denominator). To determine the quotient, long divide the polynomials in each case (what you have without the remainder).

Then
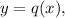`y=q(x) ,` where
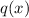`q(x)` is the quotient that provides the end behavior.

Thanks!

- Eddie