Question

Write v as a linear combination of u and w, if possible, where u = (2, 1) and

w = (2, −3).
(Enter your answer in terms of u and w. If not possible, enter IMPOSSIBLE.)
v = (4, −2)

Answer 1

Answer: v = u+w

=====================================================

Step-by-step explanation:

Let a and b take on scalar values.

v = au + bw

v = a(2,1) + b(2,-3)

v = (2a, 1a) + (2b, -3b)

v = (2a+2b, 1a-3b)

Set this equal to (4, -2) and equate components

(2a+2b, 1a-3b) = (4, -2)

2a+2b = 4 and 1a-3b = -2

We have this system of equations

`\begin{cases}2a+2b = 4\\1a-3b = -2\end{cases}`

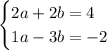
Multiply everything in the second equation by -2

So we go from 1a-3b = -2 to -2a+6b = 4

We have this equivalent system of equations

`\begin{cases}2a+2b = 4\\-2a+6b = 4\end{cases}`

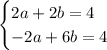
Add straight down

• The 'a' terms combine to 2a+(-2a) = 0a = 0; the 'a' variable has been eliminated.
• The 'b' terms combine to 2b+6b = 8b
• The right hand sides combine to 4+4 = 8

We then have 8b = 8 which solves to b = 1

Use this to find 'a'

2a+2b = 4

2a+2(1) = 4

2a+2 = 4

2a = 4-2

2a = 2

a = 2/2

a = 1

We found that a = 1 and b = 1

Therefore,

v = au + bw

v = 1u + 1w

v = u + w

v = 1*(2,1) + 1*(2,-3)

v = (1*2, 1*1) + (1*2, 1*(-3))

v = (2, 1) + (2, -3)

v = (2+2, 1-3)

v = (4, -2)

which confirms the answer.