Answer:
a. y=1.55(2013)-3105.3= 14.85.
b. y=1.55(2015)-3105.3= 17.95.
Explanation:
On question b we have a glance of what the problem is asking for when it says "increasing in a linear patter". This means that we can craft a mathematical function that represents these values.
Say the years are the variable x and the annual sales (in millions) are the y variable. The problem gives us 2 points of this function:
(2012, 13.3) and (2014, 16.4)
Now, we can find both the slope and formula of the function that represent the behavior of this data.
For the slope:
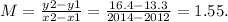
Now, let's find the formula of this function:
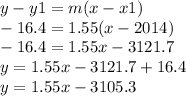
Now that we have the function of this data, let's calculate a value for the year 2013.
a. y=1.55(2013)-3105.3= 14.85.
b. y=1.55(2015)-3105.3= 17.95.