At time
 (in hours), train W travels a distance of
(in hours), train W travels a distance of

away from Abbington. Meanwhile, train X starts 150 mi away from Abbington and is getting closer, so its distance from Abbington is
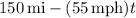
When the two trains meet, we have
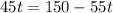
Solve for
 .
.
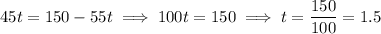
The trains pass each other after 1.5 hours, at which point train W will have traveled a distance of
