Question

A particle moves in a straight line so that, t seconds after passing a fixed point O, its displacement, s m, from O is given by

s = 1 + 3t - cos 5t.

(1) Find the distance between the particle's first two positions of instantaneous rest

(ii) Find the acceleration when t = T.​

Answer 1

(i) Differentiate
`s` with respect to
`t` to recover the particle's velocity function.

`s(t) = 1 + 3t - \cos(5t) \implies s'(t) = 3 + 5 \sin(t)`

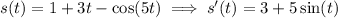
The is at rest any at time
`t` such that
`s'(t)=0`. Solve for
`t`.

`3 + 5 \sin(t) = 0 \implies \sin(t) = -\frac35 \\\\ \implies t = \sin^(-1)\left(-\frac35\right) + 2n\pi \text{ or } \pi - \sin^(-1)\left(\frac35\right) + 2n\pi`

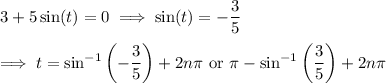
where
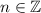`n\in\Bbb Z`. The first two times this happens occurs when

`t_1 = \pi - \sin^(-1)\left(-\frac35\right) \approx 3.78509`

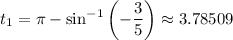
and

`t_2 = \sin^(-1)\left(-\frac35\right) + 2\pi \approx 5.63968`

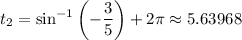
Then the distance between these positions is

`|s(t_2) - s(t_1)| \approx |18.9162 - 11.3582| \approx 7.558`

(Don't forget units.)

(ii) Not sure if you meant to specify a numerical value of
`t`, like
`t=\pi`, or an arbitrary time
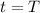`t=T`. Either way, just differentiate the velocity function to get the acceleration, and evaluate at this time.

`s'(t) = 3 + 5 \sin(t) \implies s''(t) = 5\cos(t)`

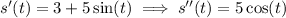
If
`t=\pi`, then
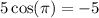`5\cos(\pi)=-5`, for instance.