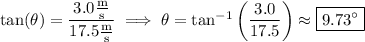Differentiate the components of position to get the corresponding components of velocity :
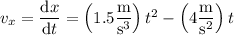
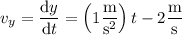
At t = 5.0 s, the particle has velocity
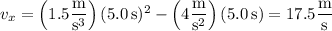
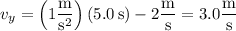
The speed at this time is the magnitude of the velocity :
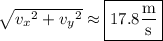
The direction of motion at this time is the angle
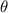 that the velocity vector makes with the positive x-axis, such that
that the velocity vector makes with the positive x-axis, such that