Question

A particle's trajectory is described by x = (0.5t^3-2t^2) meters and y = (0.5t^2-2t), where time is in seconds. What is the particle's speed at t=5.0s ? What is the particle's direction of motion, measured as an angle from the x-axis, at t=5.0s ?

Answer 1

Differentiate the components of position to get the corresponding components of velocity :

`v_x = (\mathrm dx)/(\mathrm dt) = \left(1.5(\rm m)/(\mathrm s^3)\right) t^2 - \left(4(\rm m)/(\mathrm s^2)\right)t`

`v_y = (\mathrm dy)/(\mathrm dt) = \left(1(\rm m)/(\mathrm s^2)\right)t-2(\rm m)/(\rm s)`

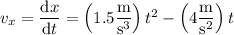
At t = 5.0 s, the particle has velocity

`v_x = \left(1.5(\rm m)/(\mathrm s^3)\right) (5.0\,\mathrm s)^2 - \left(4(\rm m)/(\mathrm s^2)\right)(5.0\,\mathrm s) = 17.5(\rm m)/(\rm s)`

`v_y = \left(1(\rm m)/(\mathrm s^2)\right)(5.0\,\mathrm s)-2(\rm m)/(\rm s) = 3.0(\rm m)/(\rm s)`

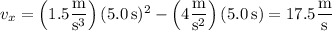
The speed at this time is the magnitude of the velocity :

`\sqrt{{v_x}^2 + {v_y}^2} \approx \boxed{17.8(\rm m)/(\rm s)}`

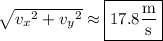
The direction of motion at this time is the angle
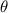`\theta` that the velocity vector makes with the positive x-axis, such that

`\tan(\theta) = (3.0(\rm m)/(\rm s))/(17.5(\rm m)/(\rm s)) \implies \theta = \tan^(-1)\left((3.0)/(17.5)\right) \approx \boxed{9.73^\circ}`