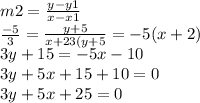Question

Find the equation of the line that passed through the point of intersection of 4x + y = -13, 3x - 4y = 14 and is parallel to the line 5x + 3y - 4 = 0.

Answer 1

3y + 5x + 25 = 0

Explanation:

Step 1: Find the coordinates of intersection of the two lines by solving the two equations.

4x + y = -13

3x - 4y = 14

Step 2: To eliminate y, make the coefficient equal, add if the variable have the different sign and subtract if the have the same sign.

4x + y = -13 ---(1) x 4

3x - 4y = 14 ---(2) x 1

16x + 4y = -52

3x - 4y = 14

19x = -38

x = -38/19 = -2

Step 3: Substitute x = -2 to find y.

3x - 4y = 14

3(-2) - 4y = 14

-6 - 4y = 14

-4y = 14 + 6

-4y = 20

`y = (20)/(-4) = -5`

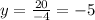
Step 4:

Therefore, the point of intersection is (x,y) = (-2,-5)

Hence the line passes through the point (-2, -5)

Step 6: since the line that passes through (-2, -5) is parallel to 5x + 3y - 4 = 0, the slope will the equal to the slope of 5x + 3y - 4 = 0

For parallel lines

m1 = m2

5x + 3y - 4 = 0

3y = -5x + 4

`y = (-5)/(3) + (4)/(3)`

m1 = -5/3

m2 = -5/3

`m2 = (y - y1)/(x - x1) \\(-5)/(3) = (y + 5)/(x + 2\\3(y+5) = -5(x + 2)\\3y + 15 = -5x - 10\\3y + 5x + 15 + 10 = 0\\3y + 5x + 25 = 0`