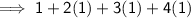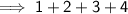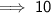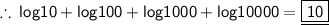• Some of the properties of the log are as follows :
1) Product law -

2) Division law -
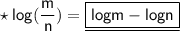
3) Power law -
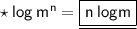
4) We should also know that -
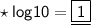
• To prove R.H.S equals to L.H.S, there exists three conditions :
1) To make R.H.S equals to L.H.S
2) To make L.H.S equals to R.H.S
3) To simplify both side equations and make them equal to a single value
In proving these questions, we're going to apply 2nd condition though all the three conditions described above are convertible to each other.
Now, let's start!


Taking L.H.S
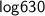
✦ Prime factors of 630 -
![\begin{gathered}\begin{gathered}{\begin{array}c2&630 \\ \hline 3&315 \\ \hline 3&105\\ \hline5&35 \\ \hline 7&7\\ \hline &1\end{array}}\end{gathered}\end{gathered}]()
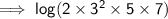
• Using first property
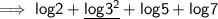
• Using third property
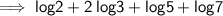
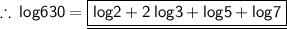

Taking L.H.S
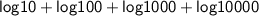
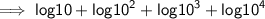
• Using third property
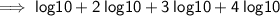
• As we know log10 = 1