Answer:

Explanation:
Given expression
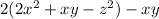
Given information
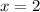
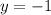
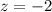
Substitute values into the given expression
![2[2(2)^2+(2)(-1)-(-2)^2]-(2)(-1)](https://img.qammunity.org/2023/formulas/mathematics/high-school/w527qty2iakh71i4bq1th36t59wdcwyq3g.png)
Simplify the exponents
![2[2(4)+(2)(-1)-(4)]-(2)(-1)](https://img.qammunity.org/2023/formulas/mathematics/high-school/g1g3zljlnvnn95hy1mplpmwo46an6pvb2w.png)
Simplify by multiplication
![2[8-2-4]+2](https://img.qammunity.org/2023/formulas/mathematics/high-school/czhcnuqti5gkacrjbmije1hs6e3ja3gg3b.png)
Simplify values in the parenthesis
![2[6-4]+2](https://img.qammunity.org/2023/formulas/mathematics/high-school/53iy29em81j8nt7savvvvkfyl1ghbz5zcz.png)
![2[2]+2](https://img.qammunity.org/2023/formulas/mathematics/high-school/fpfc73q139zeyrke4og5xpw1ho4kv26y0q.png)
Simplify by multiplication
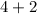

Hope this helps!! :)
Please let me know if you have any questions